如图矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,则PQ的长是()cm
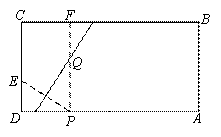
- A.
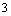
- B.
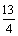
- C.
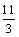
- D.4
答案
正确答案:B
知识点:图形的轴对称性
对于折叠问题,折叠问题关注对称轴,关注已知角和已知边,并要去发现已知的角和边如何跟要求的量建立联系;比如在这道题中,要求PQ的长,注意到PQ经过折叠之后到哪里了,自然就会连接EQ,转化为求EQ的长,接下来要求EQ,已知的是PD和ED,要利用这两条线段长,就需要过点Q向CD作垂线QG,则QG=PD=3,并且注意到PQ=QE=GD,可设EQ=x,则GE=x-2,在直角三角形QGE中利用勾股定理即可求出x的值,进而得到正确选项为B.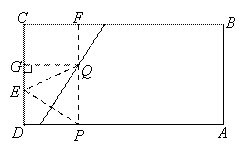
略








