已知：如图，AB∥CD，点E在AC上．
求证：∠A=∠CED+∠D．则下列证明过程错误的是(    )

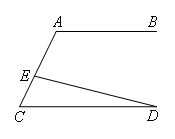
• A.证明：如图，∵∠A+∠C=180°（两直线平行，同旁内角互补）∴∠A=180°-∠C（等式的性质）
  ∵∠C+∠CED+∠D=180°（三角形的内角和等于180°）∴∠CED+∠D=180°-∠C（等式的性质）
  ∴∠A=∠CED+∠D（等量代换）
• B.证明：如图，∵∠C+∠CED+∠D=180°（三角形的内角和等于180°）∴∠CED+∠D=180°-∠C（等式的性质）
  ∵AB∥CD（已知）
  ∴∠A+∠C=180°（两直线平行，同旁内角互补）
  ∴∠A=180°-∠C（等式的性质）
  ∴∠A=∠CED+∠D（等量代换）
• C.证明：如图，∵AB∥CD（已知）
  ∴∠A+∠C=180°（两直线平行，同旁内角互补）∵∠CED+∠D+∠C=180°（三角形的内角和等于180°）∴∠A+∠C=∠CED+∠D+∠C（等量代换）
  ∴∠A=∠CED+∠D（等式的性质）
• D.证明：如图，∵AB∥CD（已知）
  ∴∠A+∠C=180°（两直线平行，同旁内角互补）
  ∴∠A=180°-∠C（等式的性质）
  ∵∠C+∠CED+∠D=180°（三角形的内角和等于180°）∴∠CED+∠D=180°-∠C（等式的性质）
  ∴∠A=∠CED+∠D（等量代换）

答案

正确答案：A

知识点：平行线的性质  三角形内角和定理  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>