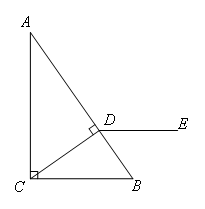
已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE∥BC,∠EDB=55°,求∠ACD的度数.
解:如图,
∵DE∥BC(已知)
∴∠B=∠EDB(两直线平行,内错角相等)
∴∠ACD=∠EDB(等量代换)
∵∠EDB=55°(已知)
∴∠ACD=55°(等量代换)
①∵∠ACB=90°(已知)
②∵CD⊥AB(已知)
③∴∠A+∠B=90°(直角三角形两锐角互余)
④∴∠B=∠ACD(同角的余角相等)
⑤∴∠ADC=90°(垂直的定义)
⑥∴∠A+∠ACD=90°(直角三角形两锐角互余)
横线处应填写的过程,顺序正确的是( )
- A.①③②⑤⑥④
- B.①②③⑤⑥④
- C.③①②⑥⑤④
- D.②①③⑥⑤④
答案
正确答案:A
知识点:直角三角形两锐角互余 同角的余角相等
如图,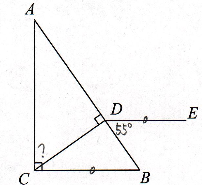
第一步:读题标注;
第二步:从条件出发,已知∠ACB=90°,
根据直角三角形两锐角互余,得∠A+∠B=90°.
又已知CD⊥AB,根据垂直的定义得到∠ADC=90°,
再根据直角三角形两锐角互余,得∠A+∠ACD=90°,
则根据同角的余角相等,得∠B=∠ACD,
又已知DE∥BC,利用两直线平行,内错角相等,得∠B=∠EDB,
由等量代换得∠ACD=∠EDB,结合已知∠EDB=55°,可得∠ACD=55°,
所以空缺处依次应填写①③②⑤⑥④.
故选A.
略








