已知：如图，AC，EF相交于点O，∠E=∠F，∠1=∠2．
求证：AB∥DG．

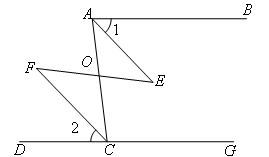
证明：如图，

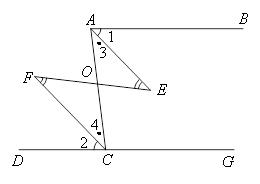
∵∠E=∠F（已知）
∴            （内错角相等，两直线平行）
∴∠3=∠4（                    ）
∵∠1=∠2（已知）
∴∠1+∠3=∠2+∠4（等式性质）
即∠BAC=∠DCA
∴            （内错角相等，两直线平行）
①AB∥DG；②AE∥CF；③两直线平行，内错角相等；
④内错角相等，两直线平行；⑤两直线平行，同位角相等．
以上空缺处依次所填正确的是(    )

• A.①④①
• B.②③⑤
• C.②③①
• D.①③②

答案

正确答案：C

知识点：平行线的性质  平行的判定  

第一个空：
条件是∠E=∠F，结合下面的推理过程以及这一步的依据是内错角相等，两直线平行，所以应填AE∥CF，所以选②；
第二个空：
条件是上一步得到的结论AE∥CF，结论是∠3=∠4，由平行得到内错角相等，所以应填的依据是两直线平行，内错角相等，所以选③；
第三个空：
条件是上一步得到的结论∠BAC=∠DCA，以及这一步的依据是内错角相等，两直线平行，所以应填AB∥DG，所以选①．
故选C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>