已知：如图，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，且BD=CD．
（1）求证：BE=CF．

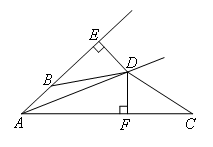
证明：如图，
∵AD平分∠BAC，DE⊥AB，DF⊥AC
∴
∠DEB=∠DFC=90°
在Rt△DEB和Rt△DFC中

∴
∴BE=CF
请你仔细观察下列序号所代表的内容：
①DE=DF；②∠EAD=∠FAD；③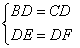；④；
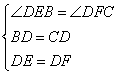⑤Rt△DEB≌Rt△DFC（HL）；⑥Rt△DEB≌Rt△DFC（SSA）．
以上空缺处依次所填最恰当的是(    )

答案

正确答案：D

知识点：略

由题中条件AD平分∠BAC，DE⊥AB，DF⊥AC，
想到角平分线性质定理，可得DE=DF，
由垂直得到∠DEB=∠DFC=90°，
又已知BD=CD，可证得Rt△DEB≌Rt△DFC（HL），
进而证得BE=CF．
空缺处依次所填应为①③⑤．
故选D．

略

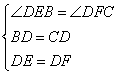下载次数：0