如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC,CE,EF,AF,则下面描述正确的是( )

- A.四边形ACEF是平行四边形,它的周长是4
- B.四边形ACEF是矩形,它的周长是
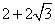
- C.四边形ACEF是平行四边形,它的周长是
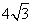
- D.四边形ACEF是矩形,它的周长是
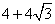
答案
正确答案:B
知识点:略
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
又∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=1,∠ACB=60°,
∴∠ACD=60°.
∵DE=AD,DF=CD,
∴四边形ACEF是平行四边形,
又∵CD=AD,
∴AD+DE=CD+DF,
即AE=CF,
∴平行四边形ACEF是矩形.
在Rt△ACF中,∠CAF=90°,∠ACD=60°,AC=1,
∴∠AFC=30°,
∴CF=2,AF=![]() ,
,
∴C矩形ACEF=2(AC+AF)=![]() .
.
略








