如图,已知△ABC为等边三角形,D为BC延长线上的点,CE平分∠ACD,CE=BD,连接AD,AE,DE.求证:△ADE为等边三角形.

证明:如图,
∵△ABC为等边三角形,
∴AB=AC,∠B=∠ACB=∠BAC=60°.
∴∠ACD=120°.
∵CE平分∠ACD,
在△ABD和△ACE中
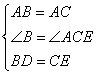
∴△ABD≌△ACE(SAS).
∴AD=AE,∠BAD=∠CAE.
∴△ADE为等边三角形( ).
① ;②
;② ;③∴∠BAC=∠DAE=60°;④∴∠ADE=∠AED;
;③∴∠BAC=∠DAE=60°;④∴∠ADE=∠AED;
⑤三个角都相等的三角形是等边三角形;⑥有一个角是60°的等腰三角形是等边三角形.
以上空缺处依次所填最恰当的是( )
- A.①④⑤
- B.①③⑥
- C.②④⑥
- D.②③⑤
答案
正确答案:B
知识点:略
要证明△ADE为等边三角形,根据已知条件考虑放到△ABD和△ACE两个三角形证全等,再证明∠DAE=60°,根据“有一个角是60°的等腰三角形是等边三角形”判定△ADE为等边三角形.
∵△ABC为等边三角形,
∴AB=AC,∠B=∠ACB=∠BAC=60°.
∴∠ACD=120°.
∵CE平分∠ACD,
在△ABD和△ACE中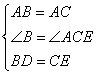
∴△ABD≌△ACE(SAS).
∴AD=AE,∠BAD=∠CAE.
∴∠BAC=∠DAE=60°
∴△ADE为等边三角形(有一个角是60°的等腰三角形是等边三角形).
故选B.
略








 ;③∴∠BAC=∠DAE=60°;④∴∠ADE=∠AED;
;③∴∠BAC=∠DAE=60°;④∴∠ADE=∠AED;