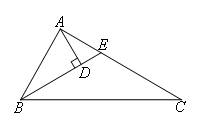
如图，在△ABC中，∠ABC=2∠C，BE平分∠ABC交AC于E，AD⊥BE于D，有下列结论：①AC-BE=AE；②∠BAD-∠C=∠DAE；③∠DAE=∠C．其中正确的是(    )

①如图，∵BE平分∠ABC，
∴
∵∠ABC=2∠C
∴∠ABE=∠CBE=∠C
∴BE=CE
∴AC-BE=AC-CE=AE，故①正确；
②如图，延长AD交BC于点F．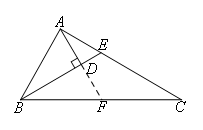

∵BE平分∠ABC，AD⊥BE
∴△ABF是等腰三角形，且AB=BF，
∴∠BAD=∠AFB
∵∠AFB是△AFC的外角，
∴∠AFB=∠C+∠DAE
∴∠BAD=∠C+∠DAE
即∠BAD-∠C=∠DAE，即②正确；
没有条件可以证明③成立，
∴③错误．
∴正确的是①②．
故选A

略