如图，OP平分∠AOB，点C，D分别在OA，OB上，且PC=PD，则∠PCO，∠PDO之间的数量关系为( )
- A.∠PCO+∠PDO=180°
- B.∠PCO=∠PDO
- C.∠PCO+∠PDO=90°
- D.∠PCO=2∠PDO
答案
正确答案：A
知识点：略
证明：如图，过点P作PE⊥OA于点E，PF⊥OB于点F．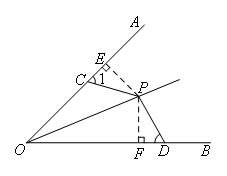
∵OP平分∠AOB，PE⊥OA，PF⊥OB
∴PE=PF，∠PEC=∠PFD=90°
在Rt△PEC和Rt△PFD中
∴Rt△PEC≌Rt△PFD（HL）
∴∠1=∠PDO
∵∠PCO+∠1=180°
∴∠PCO+∠PDO=180°
故选A．
略
WORD格式（