如图：Rt△ABC中，∠C=90°，∠A=22.5°，DC=BC，DE⊥AB．求证：AE=BE．
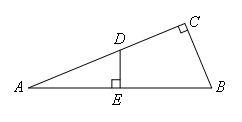
证明：如图，连接BD．
∵DC=BC
∴∠CDB=∠CBD
∵∠C=90°
∴∠CDB=∠CBD=45°
∵∠C=90°，∠A=22.5°
∴∠ABC=67.5°
∴∠DBA=∠ABC-∠CBD
=67.5°-45°
=22.5°
∴AD=BD
①DE⊥AB；②∠A=∠DBA；③
；④
．
以上空缺处依次所填最恰当的是( )
；④
．- A.①③
- B.②③
- C.①④
- D.②④
答案
正确答案：B
知识点：略
要证AE=BE，可以连接BD，将其放在△ABD中，
只要证出△ABD是等腰三角形，就可以利用等腰三角形
三线合一证出AE=BE．
已知DC=BC，由等边对等角可知∠CDB=∠CBD，
因为∠C=90°，所以∠CDB=∠CBD=45°，∠ABC=90°-∠A=67.5°，
进而求得∠DBA=∠ABC-∠CBD=22.5°，所以∠A=∠DBA，
由等角对等边可得AD=BD，又因为DE⊥AB，
利用等腰三角形三线合一可证得AE=BE．
因此空缺处依次填写最恰当的是②③．
故选B．
略
WORD格式（