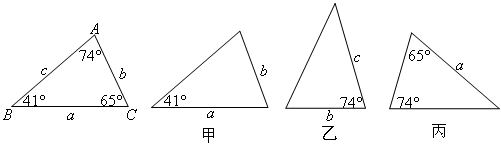
如图，已知△ABC的三边长和角度，下面甲、乙、丙3个三角形中标出了一部分边和角，其中能证明与△ABC全等的三角形是(    )

根据全等三角形判定定理，要证全等首先要找三组条件，其中必有一组边，找到三组条件之后，再根据全等三角形的判定定理逐个验证．
甲：与△ABC有两组边对应相等，还有一组角相等．
观察这三组条件在图中的位置，相等的角不是两边夹角，
所以甲三角形与△ABC不一定全等；
乙：观察三组条件在图中的位置，与△ABC有两组边对应相等，
且夹角也相等，可根据判定定理SAS得乙三角形与△ABC全等；
丙：观察三组条件在图中的位置，与△ABC有两组角对应相等，
一组边对应相等，可根据判定定理AAS得丙三角形与△ABC全等．
综上，和△ABC全等的三角形是乙和丙．
故选C．

略