已知:如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F.求证:△AED≌△AFD
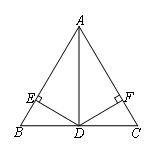
证明:如图,
在△AED和△AFD中
∴△AED≌△AFD(AAS)
①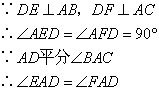 ;②
;②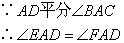 ;③
;③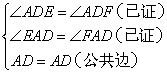 ;
;
④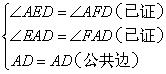 ;⑤
;⑤ .
.
以上空缺处依次所填最恰当的是( )
- A.①③
- B.①④
- C.①⑤
- D.②⑤
答案
正确答案:B
知识点:全等三角形的判定
1.解题思路
要证△AED≌△AFD,需要找三组条件:题中没有直接给出条件,
但是根据题中给出的角平分线和垂直关系,
可以得到∠EAD=∠FAD,∠AED=∠AFD两组角相等,
观察图形可知AD是公共边,因此用AAS证明三角形全等.
2.解题过程
证明:如图,
∵DE⊥AB,DF⊥AC
∴∠AED=∠AFD=90°
∵AD平分∠BAC
∴∠EAD=∠FAD
在△AED和△AFD中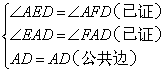
∴△AED≌△AFD(AAS)
因此,空缺处依次填写最恰当的是①④,
故选B.
略








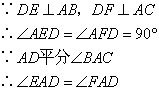 ;②
;②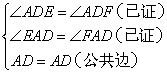 ;
;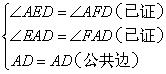 ;⑤
;⑤ .
.