已知：如图，∠ACB=∠ABC=60°，∠EDF=60°，BD=CD，∠DBC=∠DCB=30°．
求证：EF=BE+CF．

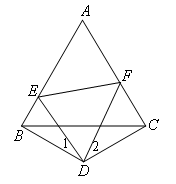
先在图上走通思路后再填写空格内容：
①要证明EF=BE+CF，是线段的和差倍分，考虑         ，解决本题用的是     ；
②结合已知条件∠ACB=∠ABC=60°，∠DBC=∠DCB=30°，BD=CD，考虑                               （辅助线），然后证全等，理由是       ，由全等的性质得         ，为接下来的全等准备条件；
③由已证的全等和条件∠EDF=60°，∠BDC=120°，得        ，然后证全等，理由是       ，由全等的性质得         ，从而得EF=BE+CF．
以上空缺处依次所填最恰当的是(    )

A.①截长补短；补短②延长AC到G，使CG=BE，连接DG；SAS；DE=DG，∠1=∠CDG③∠EDF=∠GDF；SAS；EF=GF
B.①截长补短；截长②在EF上截取EG，使EG=BE，连接DG；SAS；BD=GD，∠1=∠EDG③∠GDF=∠CDF；SAS；FG=FC
C.①截长补短；补短②延长AC到G，使CG=BE，连接DG；ASA；DE=DG③∠EDF=∠GDF；SAS；EF=GF
D.①截长补短；截长②在FE上截取FG，使FG=FC，连接DG；SAS；DC=DG，∠2=∠FDG③∠GDE=∠BDE；SAS；EG=BE

答案

正确答案：A

证明：如图，延长AC到G，使CG=BE，连接DG．

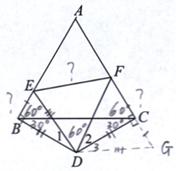
∵∠ACB=∠ABC=60°，∠DBC=∠DCB=30°
∴∠EBD=∠DCF=90°
∴∠EBD=∠DCG=90°
在△BDE和△CDG中

∴△BDE≌△CDG（SAS）
∴∠1=∠3，DE=DG
∵∠DBC=∠DCB=30°
∴∠BDC=120°
∵∠EDF=60°
∴∠1+∠2=60°
∴∠3+∠2=60°
即∠GDF=60°
∴∠EDF=∠GDF
在△EDF和△GDF中

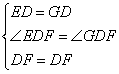
∴△EDF≌△GDF（SAS）
∴EF=FG
∵FG=FC+CG
∴EF=BE+CF
故选A．

略

下载次数：0

WORD格式（含答案版下载无答案版下载）

<<上一题