已知函数f(x)=x2-2x,g(x)=ax+2(a>0),若对任意的x1∈[-1,2],都存在x2∈[-1,2],使得f(x1)=g(x2),则实数a的取值范围是( )
- A.
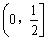
- B.
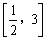
- C.(0,3]
- D.[3,+∞)
答案
正确答案:D
知识点:函数的值域
∵函数f(x)=x2-2x的图象开口向上,对称轴为直线x=1,
∴当x1∈[-1,2]时,f(x)的最小值是f(1)=-1,最大值是f(-1)=3.
∵g(x)=ax+2(a>0),且对任意的x1∈[-1,2],都存在x1∈[-1,2],
使得f(x1)=g(x2),
∴![]() ,即
,即![]()
解得a≥3.
故选D.
略







