（2020玉林）如图，四边形ABCD中，对角线AC与BD交于点O，且OA=OB=OC=OD=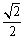AB．
（1）求证：四边形ABCD是正方形；
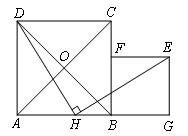
（2）若H是边AB上一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90°，得到线段HE，过点E分别作BC及AB延长线的垂线，垂足分别为F，G．设四边形BGEF的面积为S₁，以HB，BC为邻边的矩形的面积为S₂，且S₁=S₂．当AB=2时，求AH的长．

（1）证明：∵OA=OB=OC=OD，
∴AC=BD，
∴平行四边形ABCD是矩形，
∵OA=OB=OC=OD=B，
∴OA²+OB²=AB²，
∴∠AOB=90°，
即AC⊥BD，
∴四边形ABCD是正方形．
（2）解：∵EF⊥BC，EG⊥AG，
∴∠G=∠EFB=∠FBG=90°，
∴四边形BGEF是矩形，
∵将线段DH绕点H顺时针旋转90°，得到线段HE，
∴∠DHE=90°，DH=HE，
∴∠ADH+∠AHD=∠AHD+∠EHG=90°，
∴∠ADH=∠EHG，
∵∠DAH=∠G=90°，
∴△ADH≌△GHE（AAS），
∴AD=HG，AH=EG，
∵AB=AD，
∴AB=HG，
∴AH=BG，
∴BG=EG，
∴矩形BGEF是正方形，
设AH=x，则BG=EG=x，
∵s₁=s₂．
∴x²=2(2-x)，
解得：x=（负值舍去），
∴AH=．

略