如图，平行四边形ABCD的对角线AC与BD相交于点O，点E为AO的中点，过点A作AF∥BD交BE的延长线于点F，连接DF．
（1）求证：四边形AODF是平行四边形；
（2）填空：
①当△ACD满足条件 时，四边形AODF是菱形；
②当△ACD满足条件 时，四边形AODF是矩形．
答案
（1）证明略；
（2）①∠ADC=90°；②AD=CD．
知识点：特殊平行四边形的性质和判定
（1）证明：∵四边形
是平行四边形，
∴
，
，
∵
，
∴
，
∵点
为
的中点，
∴
，
在
和
中，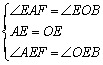
，
∴
，
∴
，
∴
，
又∵
，
∴四边形
是平行四边形．
（2）解：①
时，四边形是菱形；理由如下：
∵，，
∴
，
∵四边形是平行四边形，
∴平行四边形是菱形，
故答案为：；
②当
满足条件AD=CD时，四边形是矩形，理由如下：
∵AD=CD，，
∴
，
∴
，
∵四边形是平行四边形，
∴平行四边形是矩形，
故答案为：AD=CD．
略
WORD格式（
