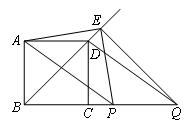
如图,BD是正方形ABCD的对角线,BC=2,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,同时动点Q从点C出发,以相同的速度沿射线BC运动,当点P出发后,过点Q作QE⊥BD,交直线BD于点E,连接AP,AE,PE,QD,设运动时间为t(秒).
(1)请直接写出动点P运动过程中,四边形APQD是什么四边形?
(2)请判断AE,PE之间的数量关系和位置关系,并加以证明.
(3)设△EPB的面积为y,求y与t之间的函数关系式.
答案
(1)四边形APQD是平行四边形;
(2)AE=PE,AE⊥PE,证明略;
(3)y与t之间的函数关系式为![]() .
.
知识点:特殊平行四边形的性质和判定
(1)四边形![]() 是平行四边形;理由如下:
是平行四边形;理由如下:
∵四边形![]() 是正方形,
是正方形,![]() ,
,![]() 速度相同,
速度相同,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)![]() ,
,![]() ;理由如下:
;理由如下:
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,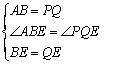 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,如图1所示:
,如图1所示:![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
略








