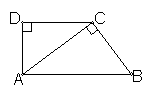
如图，梯形ABCD中，AB∥CD，AD⊥CD，若腰BC=15，对角线AC=20，且AC⊥BC，则AB=_______，AD=_______，CD=______，
= ________.
答案
25；12；16；246
知识点：直角梯形
在Rt△ACB中运用勾股定理，即AB²=AC²+BC²，把BC=15，AC=20代入可得AB=25.因为AB∥CD，AD⊥AB，根据两平行线间距离处处相等可知AD的长度与Rt△ABC斜边上的高相等。由Rt△ABC面积不变可得AB·AD=
AC·BC，解出AD=12。在Rt△ADC中，CD²=AC²-AD²，代入AC、AD的长度可得CD=16，所以
=（CD+AB）·AD=246。
对梯形的性质掌握不熟练
WORD格式（
