在△ABC中，AB=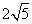
，AC=4，BC=2，以AB为边在C点的异侧作等腰直角三角形△ABD，使AB为△ABD斜边，则线段CD的长为（）
- A.
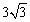
- B.
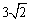
- C.
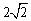
- D.3
答案
正确答案：B
知识点：双垂直模型
解：如图，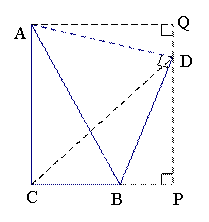
当
90°时：连接CD，过点D作BC边上的高线DP，交CB的延长线于点P，过点A作直线PD边上的高线AQ，交PD于点Q∵AB=
，AC=4，BC=2∴
，
90°又∵DE⊥CE，△ABD为等腰直角三角形∴AD=BD，
90°，
90°，
90°∴
∴△QAD≌△PDB∴AQ=DP，DQ=BP设BP=DQ=x，则AQ=2+x，PD=PQ-PD=4-x∵AQ=PD∴2+x=4-x，x=1∴DP=PC=3∴在Rt△DPC中，CD=
=
略
WORD格式（
