在等边三角形ABC中，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB，交直线DN于点F．
（1）如图1，当点D在线段BC上，∠NDB为锐角时，线段CF，BE，CD之间的数量关系是 ．（提示：过点F作FM∥BC，交射线AB于点M）( )
- A.CF+BE=CD
- B.CF-BE=CD
- C.BE-CF=CD
- D.BE-CF=
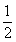CD
答案
正确答案：A
知识点：略
过点F作FM∥BC，交射线AB于点M
∵三角形ABC是等边三角形
∴∠ABC=∠ACB=60°，AC=BC
∵∠ADN=60°
∴∠CDF+∠ADC=120°，∠ADC+∠DAC=120°
∴∠CDF=∠DAC
∵CF∥AB，FM∥BC
∴四边形BMFC是平行四边形
∴MF=BC=AC，BM=CF,∠EMF=∠ABC=∠ACB，∠MFE=∠CDF=∠DAC
∴△MEF≌△CDA
∴CD=ME=BM+BE
∴CD=CF+BE
故选A
略
WORD格式（
