如图，在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=
，∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t秒．
（1）求BC的长；
（2）当MN∥AB时，求t的值；
（3）试探究：t为何值时，△MNC为等腰三角形.
答案
（1）过点A作AK垂直BC于点K，过点D作DH垂直BC于点H，从而AK∥DH，如图①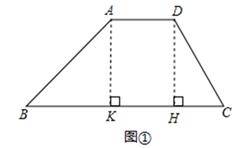
∵AK⊥BC，∠B=45°，AB=
∴AK=BK=4
∵AD//BC,AK∥DH，AK⊥BC
∴ADHD为矩形
∴AK=DH=4，KH=AD=3
∵∠DHC=90°，DC=5
∴HC=3
∴BC=BK+KH+HC=3+3+4=10
（2）依题意可知：CN=t，BM=2t，CM=10-2t（0≤t≤5），过点D作DG//AB交BC于点G，如图②，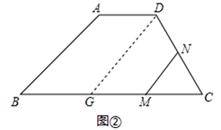
∵MN//AB
∴DG//MN
∴△GDC∽△MNC
∵AD//BG，AB//DG
∴AD=BG=3
∴GC=BC-BG=10-3=7
∵△GDC∽△MNC
∴
∵DC=5，CG=7，CN=t，CM=10-2t
∴
∴t=
∵0≤≤5
∴t=符合题意
（3）0＜t＜5分三种情况讨论：①当NC=MC时，如图③，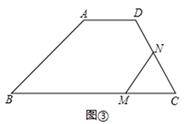
即t=10-2t，
∴t=
②当MN=NC时，如图④，过N作NE⊥MC于E，CE=
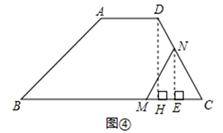
∵∠C=∠C，∠DHC=∠NEC=90°，
∴△NEC∽△DHC．
∴
即
∴t=
③当MN=MC时，如图⑤，过M作MF⊥CN于F点．FC=
NC=t．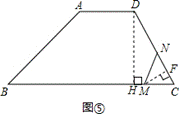
∵∠C=∠C，∠MFC=∠DHC=90°，
∴△MFC∽△DHC．
∴
即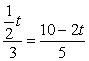
∴t=
．
由于0＜＜5，0＜＜5，0＜＜5，所以均符合题意
综上所述，当t=、t=或t=时，△MNC为等腰三角形．
知识点：相似中的动点问题
略
略
WORD格式（
