△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
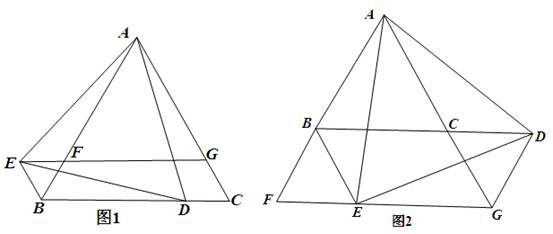
(1)如图1所示,当点D在线段BC上时.
①求证:△AEB≌△ADC
②探索四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立?
(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
答案
证明:(1)①∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°
又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC.
②由①得△AEB≌△ADC,
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,
∴EB∥GC.
又∵EG∥BC,
∴四边形BCGE是平行四边形.
(2)①②都成立.
(3)当CD=CB(∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.
证明如下:
由①得:△AEB≌△ADC,
∴BE=CD
又∵CD=CB,
∴BE=CB.
由②得四边形BCGE是平行四边形,
∴四边形BCGE是菱形.
其他条件类比可证。
略
略








