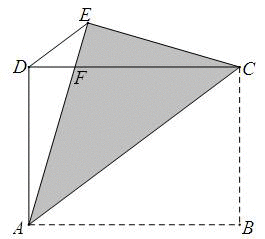
如图,在矩形ABCD中,BC=3cm,DC=4cm,将该矩形沿对角线AC折叠,使点B落在点E处,AE与边CD交于点F.
(1)求EF的长;
(2)连接DE,求四边形ACED的面积与周长各是多少?
答案
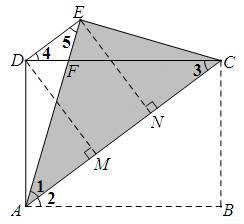
解:(1)∵四边形ABCD为矩形,BC=3cm,DC=4cm
∴AD=CE=BC=3cm,AB=AE=DC=4cm,∠AEC=∠B=90°,CD∥AB
∴![]() cm
cm
∵∠1=∠2,∠2=∠3
∴∠1=∠3
∴AF=CF
设EF=xcm,则CF=AF=(4-x)cm
在Rt△EFC中,![]() ,即
,即![]() cm 解得x=
cm 解得x=![]() cm
cm
即EF=![]() cm.
cm.
(2)由(1)可知:AF=CF
∵AE=CD
∴DF=EF
∴![]()
又∵∠DFE=∠AFC,![]()
∴∠1=∠5=∠4=∠3
∴DE∥AC
∵AD=CE=3cm,且AD与CE不平行
∴四边形ACED是等腰梯形过点D、E分别作DM⊥AC于点M、EN⊥AC于点N可证四边形DMNE为矩形,Rt△ADM≌Rt△CEN.
∴DM=EN、DE=MN
在Rt△ACE中,![]() cm=DM
cm=DM
在Rt△CEN中,![]() cm=AM
cm=AM
则DE=MN=![]() cm
cm
则四边形ACED的周长为![]() cm,面积为
cm,面积为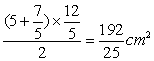
知识点:四边形、折叠问题、勾股定理
略
略








