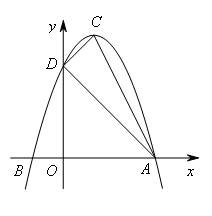
（2010山东威海）如图，抛物线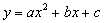的顶点为C（1，4），交x轴于点A（3，0），交y轴于点D．试探究在抛物线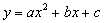上是否存在除点C以外的点E，使得△ADE与△ACD的面积相等？若存在，请求出此时点E的坐标，若不存在，请说明理由．

答案

解：存在．因为抛物线的顶点坐标是C（1，4），
所以，可设抛物线的表达式为y=
又因为抛物线经过点A（3，0），
所以将其坐标代入上式，得0=，
解得a=-1；
∴该抛物线的表达式为y=
即y=
∴D点坐标为（0，3）；
由题意，设直线AD的表达式为y=kx+3，代入点A的坐标，得0=3k+3，解得k=-1；
∴直线AD的表达式为y=-x+3；
过C点作CG⊥x轴，垂足为G，交AD于点H；
则H点的纵坐标为-1+3=2；
∴CH=CG-HG=4-2=2；
设点E的横坐标为m，则点E的纵坐标为；
过E点作EF⊥x轴，垂足为F，交AD于点P，则点P的纵坐标为3-m，EF∥CG；
若EP=CH，则△ADE与△ADC的面积相等；
①若E点在直线AD的上方，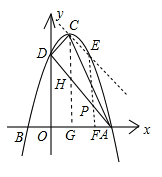

则PF=3-m，EF=，
∴EP=EF-PF=-（3-m）=；
∴=2，解得=2，=1；
当m=2时，PF=3-2=1，EF=1+2=3；
∴E点坐标为（2，3）；
同理当m=1时，E点坐标为（1，4），与C点重合；
②若E点在直线AD的下方，

则PE=（3-m）-（）=；
∴=2，解得
当时，E点的纵坐标为；
当时，E点的纵坐标为；
∴在抛物线上存在除点C以外的点E，使得△ADE与△ACD的面积相等，E点的坐标为（2，3）；（，）；（，）

知识点：中考压轴之函数类问题  

略

略

下载次数：13

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>