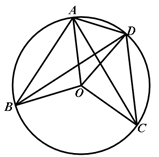
(2011浙江)如图,点A,B,C,D都在⊙O上,劣弧CD的度数等于84°,CA是∠OCD的平分线,则∠ABD十∠CAO= _______°
答案
:∵圆心角的度数和它们对的弧的度数相等,
∴ CD^的度数等于84°,即∠COD=84°;
在△COD中,OC=OD(⊙O的半径),
∴∠OCD=∠ODC(等边对等角);
又∠COD+∠OCD+∠ODC=180°,
∴∠OCD=48°;
而CA是∠OCD的平分线,
∴∠OCA=∠OCA,
∴∠OCA=∠OCA=24°;
在△AOC中,OA=OC(⊙O的半径),
∴∠CAO=∠OCA(等边对等角);
∵∠ABD= ∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∠OCA= ∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∴∠ABD=∠CAO,
∴∠ABD+∠CAO=48°;
故答案为:48°.
知识点:圆心角、弧、弦的关系 圆周角定理
在等腰△OAC和△OCD中,根据等腰三角形的两个底角相等的性质求得∠OCD=∠ODC、∠CAO=∠OCA,所以由三角形的内角和求得∠OCD=48°;然后根据角平分线的性质求得∴∠OCA=∠OCA=24°;最后由圆周角定理知:∠ABD= ∠AOD,∠OCA=
∠AOD.所以∠ABD=∠CAO,进而求得∠ABD+∠CAO=48°.
同弧所对的圆周角相等。








