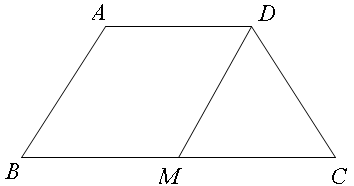
(2011四川南充)如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
(1)求证:△MDC是等边三角形;
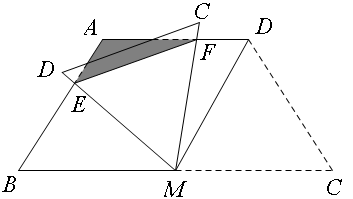
(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC')同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
答案
解:(1)过点A作AE⊥BC交BC于点E,过点D作DF⊥BC于点F
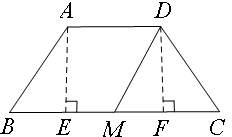
则AD=EF=2,
∵四边形ABCD为等腰梯形,∠C=60°
∴∠BAE=∠CDF=30°
∵CD=AB=2
∴CF=BE=1
从而BC=BE+EF+CF=1+2+1=4
∵M为BC的中点
∴MC=2
∴△MDC为等边三角形(有一个角为60° 的等腰三角形为等边三角形)
(2)解:连接AM,则△AMB为等边三角形
∴BM=AM,∠B=∠MAD=60°
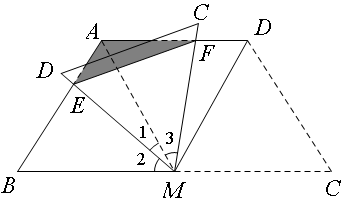
由∠1+∠2=60°,∠1+∠3=60°得:∠2=∠3
在△AMF和△BME中
∴△AMF≌△BME(ASA)
∴AF=BE,ME=MF
∵∠EMF=60°
∴△EMF为等边三角形
∴EF=EM
从而△AEF的周长=AE+AF+EF=AE+BE+EM=AB+EM=2+EM
∴要想△AEF的周长最小,只需EM最小
显然当△MDC旋转至EM⊥AB时EM最小,此时EM为等边三角形ABM的高线,故EM=
从而△AEF的周长的最小值为2+
知识点:等腰梯形的性质
转移线段,将△AEF的周长转换成已知线段长度的和的最小值
证明出△AMF≌△BME是关键









