在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(1)延长MP交CN于点E(如图2).求证:①△BPM≌△CPE;②求证:PM=PN;
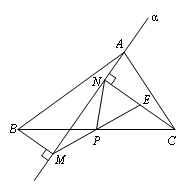
图2
小石的思路是这样的,要证明△BPM≌△CPE,只需找三组条件,首先题干中的点P为BC边中点,可以得到(),然后,题干中BM⊥直线a于点M,CN⊥直线a于点N,所以(),从而∠1=∠2,∠5=∠6,或者加上∠3=∠4,就可以得到△BPM≌△CPE,从而得到(),那么NP就是直角三角形MNE斜边中线,由直角三角形斜边中线等于斜边一半,所以NP=MP。括号里要填写的内容顺序为()①BP=PC;②MP=PE;③BM∥CN
- A.①②③
- B.②①③
- C.③②①
- D.①③②
答案
正确答案：D
知识点：类比探究问题
略
略
WORD格式（
