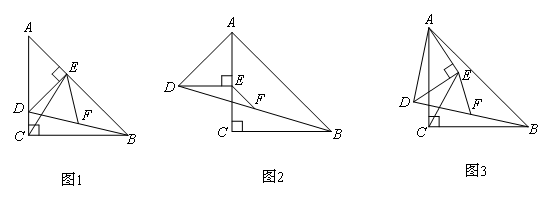
如图1，在△ACB和△AED中，AC=BC，AE=DE，∠ACB=∠AED=90°，点E在AB上，F是线段BD的中点，连接CE，FE．（1）请你探究线段CE与FE之间的数量关系；（2）将图1中的△AED绕点A顺时针旋转，使△AED的一边AE恰好与△ACB的边AC在同一条直线上（如图2），连接BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由；（3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3），连接BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由．
答案
解（1）CE＝
EF过点B作DE的平行线交EF的延长线于点G，连接CG、CF
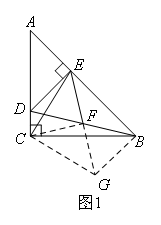
∵DE∥BG
∴∠DEF＝∠BGF，∠DEB＝∠GBE＝90°
∵∠DFE＝∠BFG，DF＝BF
∴△DEF≌△BGF
∴BG＝DE，EF＝GF
∵AE＝DE，AC＝BC
∴AE＝BG，∠ABC＝∠CAB＝45°
∴∠GBC＝45°
∴△AEC≌△BGC
∴CE＝CG，∠ACE＝∠BCG
∴∠ECG＝∠ACB＝90°，即：△ECG是等腰直角三角形
∵EF＝GF
∴△CEF是等腰直角三角形
∴CE＝EF
（2）成立理由：延长EF交BC于点G，连接CF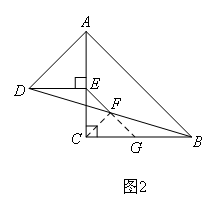
∵DE∥BC
∴∠DEF＝∠BGF
∵∠DFE＝∠BFG，DF＝BF
∴△DEF≌△BGF
∴BG＝DE，EF＝GF
∵AE＝DE，AC＝BC
∴AE＝BG
∴CE＝CG
∴△ECG是等腰直角三角形
∵EF＝GF
∴△CEF是等腰直角三角形
∴CE＝EF
（3）成立理由：过点B作DE的平行线交EF的延长线于点G，连接CG、CF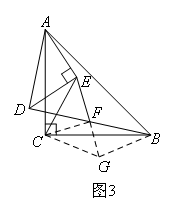
∵DE∥BG
∴∠DEF＝∠BGF
∵∠DFE＝∠BFG，DF＝BF
∴△DEF≌△BGF
∴BG＝DE，EF＝GF
∵AE＝DE
∴AE＝BG
∵AE⊥BG，AC⊥BC
∴∠EAC＝∠GBC
∵AC＝BC
∴△AEC≌△BGC
∴CE＝CG，∠ACE＝∠BCG
∴∠ECG＝∠ACB＝90°，即：△ECG是等腰直角三角形
∵EF＝GF
∴△CEF是等腰直角三角形
∴CE＝EF
知识点：四边形中的类比探究
略
略
WORD格式（
