如图，在等腰梯形ABCD中，AD∥BC，DE⊥BC于E，且DE=
，AD=18，∠C=60°．
（1）BC= ；
（2）若动点P从点D出发，速度为2个单位/秒，沿DA向点A运动，同时，动点Q从点B出发，速度为3个单位/秒，沿BC向点C运动，当一个动点到达端点时，另一个动点同时停止运动，设运动的时间为t秒．
①t= 秒时，四边形PQED是矩形；
②t为何值时，线段PQ与梯形ABCD的边构成平行四边形？
③是否存在t值，使②中的平行四边形是菱形？若存在，请求出t值；若不存在，请说明理由．
答案
解：（1）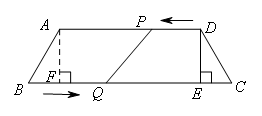
如图，过A作AF⊥BC于点F
在Rt△DEC中，∠C=60°，DE=
∴DC=8，CE=4
∵梯形ABCD为等腰梯形
∴△ABF≌△DCE
∴BF=CE=4
∵EF=AD=18
∴BC=BF+EF+CE=26
（2）①由题意知
∵BQ=3t
∴QE=BE-BQ=22-3t
∵PD=2t，QE=PD
∴2t=22-3t
即t=
②∵P，Q分别在AD，BC上，
∴PQ只能与AB、DC两边组成平行四边形
当AP=BQ时，18-2t=3t
∴t=
时，四边形ABQP为平行四边形
当PD=QC时，2t=26-3t
∴t=
时，四边形PQCD为平行四边形．
③当t=时，四边形ABQP为平行四边形此时AP=
∵AB=8
∴此时四边形ABQP不是菱形
当t=时，四边形PQCD为平行四边形
此时PD=
∵CD=8
∴四边形PQCD不是菱形
即不存在t值使得②中平行四边形是菱形．
知识点：四边形中的动点、存在性问题
略
略
WORD格式（
