如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB落在x轴正半轴上，直线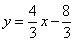经过点C，与x轴交于点E．
（1）求四边形AECD的面积；
（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；
（3）若直线l₁经过点F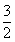（-，0）且与直线y＝3x平行，将（2）中直线l沿着y轴向上平移1个单位，交x轴于点M，交直线l₁于点N，求△NMF的面积．

答案

解：（1）∵正方形ABCD的边长是4，AB在x轴上
∴C点的纵坐标为4
代入得：C（5，4）
∴A（1，0），B（5，0），D（1，4）
∵与x轴交于点E
∴E（2，0）
∴AE＝1，CD＝4，AD＝4
∴S_{四边形AECD}＝×（1＋4）×4＝10
（2）
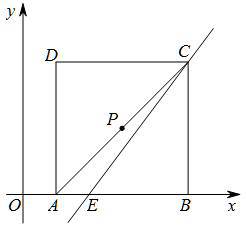
如果直线l平分正方形的面积，则l一定过正方形的中心（即对角线的中点）如图，P是对角线AC的中点
∵A（1，0），C（5，4）
∴P（3，2）
∴直线l经过点E（2，0），P（3，2）待定系数法可得直线解析式为：y＝2x－4
（3）∵直线l₁经过点F（-，0）且与直线y＝3x平行，设直线l₁的解析式为y₁＝kx＋b，则：k＝3
代入F（-，0）得：b＝
∴y₁＝3x＋
直线l沿着y轴向上平移1个单位，则所得的直线的解析式是：y＝2x-3，
∴M（，0）
联立即：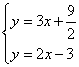
可得：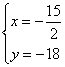
即：N（-，-18）
S_△NMF＝×[-（-）]×|-18|＝27

知识点：一次函数与几何综合  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>