如图，在直角坐标系中，O是坐标原点，A，B，C三点的坐标分别为A（18，0），B（18，8），C（6，8），四边形OABC是梯形，点P，Q同时从原点出发，分别做匀速运动，其中点P沿OA向终点A运动，速度为每秒2个单位，点Q沿路线O→C→B运动，速度为每秒3个单位，当一点到达终点则另一点也停止运动，设运动的时间为t秒．
（1）求直线OC的解析式；
（2）从运动开始，梯形被直线PQ分割后的图形中是否存在平行四边形，若存在，求出t的值，若不存在，请说明理由；
（3）当t为何值时，直线PQ把梯形OCBA分成面积为1：7的两部分？
答案
解：（1）设OC的解析式为y=kx+b，
∵O，C两点的坐标分别为O（0，0），C（6，8），
∴
解得
∴
（2）当四边形OPQC是平行四边形时
∴CQ=OP∵CQ=3t-10，OP=2t
∴3t-10=2t，
∴t=10．
∵t≤
∴不存在四边形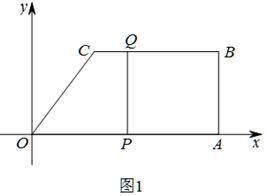
如图1，当四边形PABQ为平行四边形时
∴BQ=PA
∵BQ=22-3t，PA=18-2t
∴22-3t=18-2t
∴t=4
（4）∵A（18，0），B（18，8），C（6，8），
∴OA=18，BC=12，AB=8，
∴
=120
∵直线PQ把梯形OCBA分成面积为1：7
∴两部分的面积分别为15，105
当
=15时，即
=15
∴t=
当
=105时，即
=105
∴t=
综上可得：当t=或时直线PQ把梯形OCBA分成面积为1：7的两部分．
知识点：一次函数动点问题
略
略
WORD格式（
