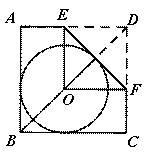
(2011浙江温州)如图,O是正方形ABCD的对角线BD上一点,⊙O与边AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF对折,折痕EF与⊙O相切,此时点D恰好落在圆心O处,若DE=2,则正方形ABCD的边长是( )
- A.3
- B.4
- C.

- D.
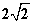
答案
正确答案:C
知识点:勾股定理 正方形的性质 切线的性质 翻折变换(折叠问题)
解:如图
延长FO交AB于点G,则点G是切点,OD交EF于点H,则点H是切点.
∵ABCD是正方形,点O在对角线BD上,
∴OG=OH=HD=HE=AE,且都等于圆的半径.
在等腰直角三角形DEH中,DE=2,
∴EH=DH=![]() =AE.
=AE.
∴AD=AE+DE=![]() +2.故选C.
+2.故选C.
本题考查的是切线的性质,利用切线的性质,结合正方形的特点求出正方形的边长.学生可能不能在翻折问题中灵活运用切线的性质.








