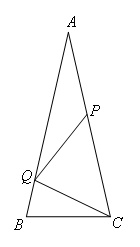
如图,在△ABC中,AB=AC,点P,Q分别在AC,AB上,且AP=PQ=QC=BC,则∠A的大小是( )
- A.30°
- B.20°
- C.
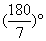
- D.25°
答案
正确答案:C
(1)考点:等腰三角形的性质;三角形内角和定理;三角形的外角性质.
(2)解题过程:
解:∵AB=AC,AP=PQ,QP=QC,QC=BC,
∴∠B=∠ACB,∠A=∠AQP,∠QPC=∠QCP,∠BQC=∠B,
设∠A=x,则∠AQP=x,
∴∠QPC=∠A+∠AQP=2x,
∴∠BQC=∠ACQ+∠A
∴∠BQC=3x,
∴∠B=3x,
∴∠ACB=3x,
∵在△ABC中,∠A+∠ACB+∠B=180°,
∴x+3x+3x=180°
解得x=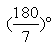
∴∠A=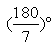
故选C
略








