如图,在做△ABC中,BC>AB>AC,∠ACB=40°,如果D,E是直线AB上的两点,且AD=AC,BE=BC,则∠DCE的度数为(    )

解：（1）如图1，当点D，E在点A的同侧，且都在BA的延长线上时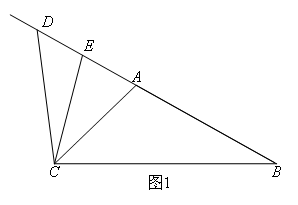

∵BE=BC
∴∠BEC=（180°-∠ABC）÷2
∵AD=AC
∴∠ADC=（180°-∠DAC）÷2=∠BAC÷2
∵∠BEC=∠ADC+∠DCE
∴∠DCE=∠BEC-∠ADC
∴∠DCE=（180°-∠ABC）÷2-∠BAC÷2
=（180°-∠ABC-∠BAC）÷2
=∠ACB÷2
=40°÷2
=20°
（2）如图2，当点D,E在点A的同侧，且点D在点D′的位置，点E在点E′的位置时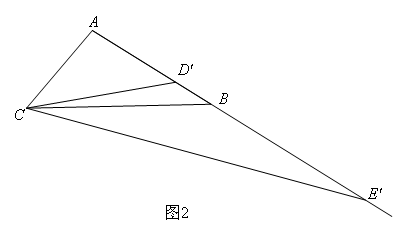

∵BE′=BC
∠ABC=∠BCE′+∠BE′C
∴∠BE′C=∠ABC÷2
∵AD′=AC
∴∠AD′C=（180°-∠BAC）÷2
∵∠AD′C=∠D′CE′+∠BE′C
∴∠D′CE′=∠AD′C-∠BE′C
∴∠D′CE′=（180°-∠BAC）÷2-∠ABC÷2
=（180°-∠BAC-∠ABC）÷2
=∠ACB÷2
=40°÷2
=20°
（3）如图3，当点D，E在点A的两侧，且点E在点E′的位置时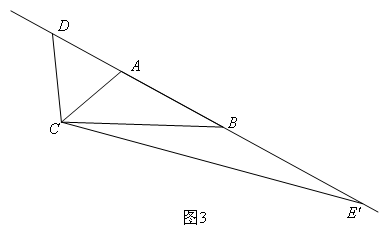

∵BE′=BC
∴∠BE′C=（180°-∠CBE′）÷2=∠ABC÷2
∵AD=AC
∴∠ADC=（180°-∠DAC）÷2=∠BAC÷2
∵∠DCE′=180°-（∠BE′C+∠ADC）
∴∠DCE′=180°-（∠ABC+∠BAC）÷2
=180°-（180°-∠ACB）÷2
=110°
（4）如图4，当点D，E在点A的两侧，且点D在点D′的位置时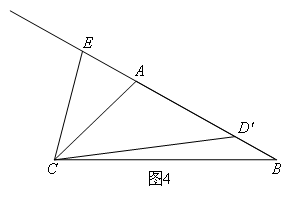

∵AD′=AC
∴∠AD′C=（180°-∠BAC）÷2
∵BE=BC
∴∠BEC=（180°-∠ABC）÷2
∴∠D′CE=180°-（∠BEC+∠AD′C）
=180°-（180°-∠ABC）÷2-（180°-∠BAC）÷2
=(∠BAC+∠ABC)÷2
=（180°-∠ACB）÷2
=（180°-40°）÷2
=70°
综上，∠DCE的度数为20°或70°或110°
故选C

略