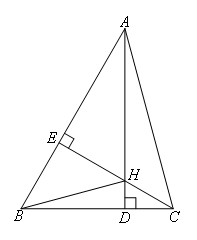
如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,且EH=EB,小彤在研究时得到四个结论:①∠ABC=45°;②AH=BC;③AE-BE=CH;④△AEC是等腰直角三角形.你认为正确的序号是(    )

①∵AD⊥BC，
若∠ABC=45°，则∠BAD=45°，由题意可知：∠BAC=45°，
所以∠ABC=45°不成立，故选项①错误；
②∵CE⊥AB，∠BAC=45°，
∴AE=EC，
在△AEH和△CEB中，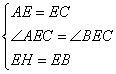

∴△AEH≌△CEB（SAS），
∴AH=BC，故选项②正确；
③又EC-EH=CH，
∴AE-EH=CH，故选项③正确．
④∵AE=CE，CE⊥AB，所以△AEC是等腰直角三角形，故选项④正确．
∴②③④正确．
故选B．

略