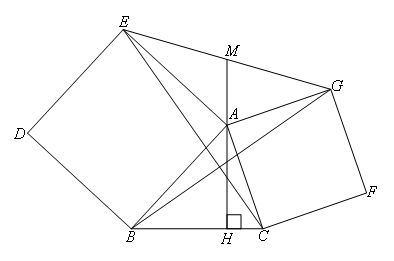
在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形ABDE和正方形ACFG,连接CE,BG和EG,EG与HA的延长线交于点M.下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;
④∠EAM=∠ABC,其中正确结论的个数是(    )

在正方形ABDE和正方形ACFG中，AB=AE，AC=AG，∠BAE=∠CAG=90°，
∴∠BAE+∠BAC=∠CAG+∠BAC，
即∠CAE=∠BAG，
∵在△ABG和△AEC中，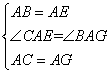

∴△ABG≌△AEC（SAS），
∴BG=CE，故①正确；
设BG，CE相交于点N，
∵△ABG≌△AEC，
∴∠ACE=∠AGB，
∵∠NCF+∠NGF=∠ACF+∠AGF=90°+90°=180°，
∴∠CNG=360°-（∠NCF+∠NGF+∠F）=360°-（180°+90°）=90°，
∴BG⊥CE，故②正确；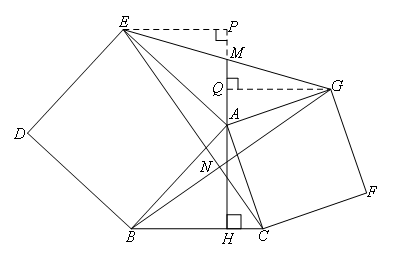

如图，过点E作EP⊥HA,交HA的延长线于P，过点G作GQ⊥AM于Q，
∵AH⊥BC，
∴∠ABH+∠BAH=90°，
∵∠BAE=90°，
∴∠EAP+∠BAH=180°-90°=90°，
∴∠ABH=∠EAP，即∠ABC=∠EAM，故④正确.
∵在△ABH和△EAP中，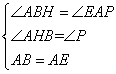

∴△ABH≌△EAP（AAS），
∴EP=AH，
同理可得GQ=AH，
∴EP=GQ，
∵在△EPM和△GQM中，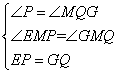

∴△EPM≌△GQM（AAS），
∴EM=GM，
∴AM是△AEG的中线，故③正确．
综上所述，①②③④都正确．
故选A．

略