如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为(    )海里/小时.

• A.
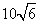
• B.
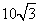
• C.
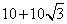
• D.

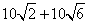
答案

正确答案：C

知识点：解直角三角形的应用—方位角问题  

如图，过点O作OG⊥AB于点G．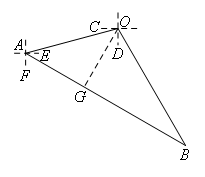

由题意得，∠AOB=105°，∠OAE=15°，∠BAE=30°，，
∴∠OAG=45°，
∴∠B=30°．
在Rt△OAG中，，∠OAG=45°，
∴OG=AG=10．
在Rt△OGB中，∠B=30°，OG=10，
∴，，
∴海里．
又∵乙船的速度为10海里/小时，
∴甲船追赶乙船的时间为1小时，
故甲船追赶乙船的速度是海里/小时．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>