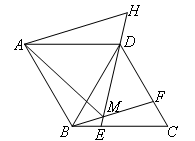
如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点M,延长ED到H使DH=BM,连接AM,AH.则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;
④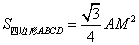.其中正确的有(    )

由题意得△ABD和△CBD是等边三角形，
容易得到△BDF≌△DCE（SAS），故①结论正确；
∵△BDF≌△DCE，
∴∠DBF=∠EDC，
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°，
∴∠BMD=120°，故②结论正确；
在四边形ABMD中，
∵∠BAD+∠BMD=180°，
∴∠ABM+∠ADM=180°，
又∵∠ADM+∠ADH=180°，
∴∠ABM=∠ADH，
∵AB=AD，DH=BM，
∴△ABM≌△ADH（SAS），
∴AH=AM，∠BAM=∠DAH，
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°，
∴△AMH是等边三角形，故③结论正确；
∵△ABM≌△ADH，
∴△AMH的面积等于四边形ABMD的面积，
∵等边△AMH的面积为，
∴，
则，故④结论错误．
综上所述，正确的是①②③共3个．

略