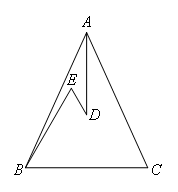
如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°.
若BE=6cm,DE=2cm,则BC=(    )

如图，延长ED交BC于点M，延长AD交BC于点N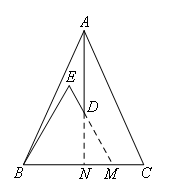

∵AB=AC，AD平分∠BAC
∴AN⊥BC，BN=CN
∵∠EBC=∠E=60°
∴△BEM为等边三角形
∵BE=6，DE=2
∴DM=4
∵∠DNM=90°，∠DMN=60°
∴∠NDM=30°
∴
∴BN=BM-MN=6-2=4
∴BC=2BN=8cm
故选D

略