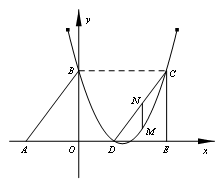
（2010四川眉山）如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为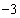（，0）、（0，4），抛物线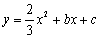经过B点，且顶点在直线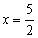上．（1）求抛物线对应的函数关系式；（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；（3）若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．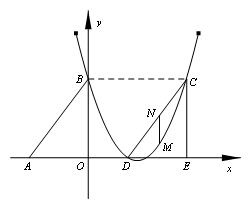

答案

解：（1）由题意，可设所求抛物线对应的函数关系式为
∴
∴
∴所求函数关系式为：
（2）在Rt△ABO中，OA=3，OB=4，
∴
∵四边形ABCD是菱形∴BC=CD=DA=AB=5
∴C、D两点的坐标分别是（5，4）、（2，0）．
当时，
当时，
∴点C和点D在所求抛物线上．
（3）设直线CD对应的函数关系式为，则解得：．
∴
∵MN∥y轴，M点的横坐标为t，
∴N点的横坐标也为t．则，，
∴
∵，
∴当时，，此时点M的坐标为（，）．

知识点：待定系数法求二次函数解析式  

（1）先根据对称轴、原表达式设出顶点式，从而计算出函数解析式；
（2）先计算出C、D坐标，然后判断是否在抛物线上；（3）利用坐标间的关系计算M、N点之间的距离；

(1)抛物线解析式计算错误;(2)M、N点的坐标表达与线段长度计算错误；

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>