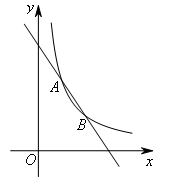
如图,已知反比例函数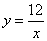 在第一象限的图象与一次函数
在第一象限的图象与一次函数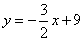 的图象交于点A,B,若在第一象限内的反比例函数图象上存在一点P,使得△AOP和△BOP的面积相等,则点P的坐标为( )
的图象交于点A,B,若在第一象限内的反比例函数图象上存在一点P,使得△AOP和△BOP的面积相等,则点P的坐标为( )
- A.
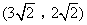
- B.
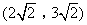
- C.
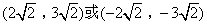
- D.
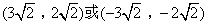
答案
正确答案:B
当点A,B位于直线OP同侧时,
∵△AOP和△BOP有公共边OP,
∴要使得![]() ,需OP∥AB,
,需OP∥AB,
即过点O作AB的平行线,与反比例函数![]() 的图象在第一象限内的交点
的图象在第一象限内的交点
就是要找的P点.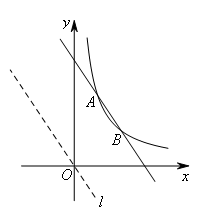
如图,直线![]() 过点O且与AB平行,结合图象可知
过点O且与AB平行,结合图象可知![]() 和反比例函数在第一象限的图象没有交点,即不存在点A,B位于直线OP同侧的情况.
和反比例函数在第一象限的图象没有交点,即不存在点A,B位于直线OP同侧的情况.
当点A,B位于直线OP异侧时,要使得![]() ,需直线OP经过线段AB的中点.
,需直线OP经过线段AB的中点.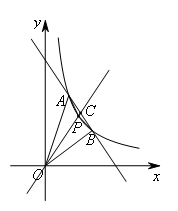
如图,点C是AB的中点,点P为直线OC与双曲线的交点.
易证![]() ,
,![]() ,
,
∴![]() .
.
由![]() 得,
得,![]() ,
,![]() ,
,
∴A(2,6),B(4,3),
∵点C是AB的中点,
由中点坐标公式可得![]() ,
,
∴直线OC的表达式为![]() .
.
联立直线OC和反比例函数的表达式可得![]() .
.
略








