如图，已知A、B两点的坐标分别为（4，0）、(0，2)，P是△AOB外接圆上的一点，且∠AOP=45°，则点P的坐标为（   ）

∵∠AOB=90°、∠AOP=45°∴∠BOP=∠AOP=45°连结PB、PA，过P分别作PC⊥OB于C、作PD⊥OA于D.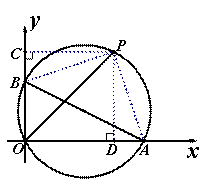

∵O、A、P、B四点共圆， ∠BOP=∠AOP
∴BP=AP、PD=PC=OD=OC
在Rt△BPC和Rt△APD中
BP=AP、PC=PD
∴Rt△BPC≌Rt△APD
∴BC=AD
∴OC+OD=OB+OA=6=2OD
∴PC=PD=OD=3
∴点P的坐标为（3，3）；

内接四边形定理应用不熟练，对圆中线段和角的转换不熟悉。