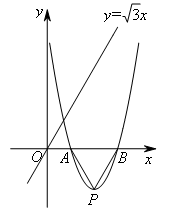
如图,已知抛物线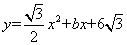 经过点A(2,0).设抛物线与x轴的另一交点为B,抛物线的顶点为P.若在直线
经过点A(2,0).设抛物线与x轴的另一交点为B,抛物线的顶点为P.若在直线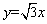 上存在点D,使四边形OPBD为平行四边形,则点D的坐标为( )
上存在点D,使四边形OPBD为平行四边形,则点D的坐标为( )
- A.
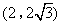
- B.
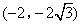
- C.
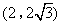 或
或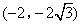
- D.
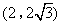 ,
,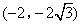 或
或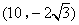
答案
正确答案:A
要使得四边形OPBD为平行四边形,分析定点、动点,O,P,B为定点,D为直线![]() 上的动点,四边形四个顶点的位置关系确定.
上的动点,四边形四个顶点的位置关系确定.
将点A的坐标代入抛物线表达式得,![]() ,解得
,解得![]() ,
,
∴抛物线的表达式为![]() ,
,
∴B(6,0),![]() .
.
易求得直线PB的表达式为![]() ,与直线
,与直线![]() 平行.
平行.
要使得四边形OPBD为平行四边形,需OP∥BD.
如图,过点B作OP的平行线,与直线![]() 的交点即为点D.
的交点即为点D.
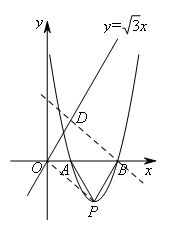
由O(0,0),![]() 可得直线OP的表达式为
可得直线OP的表达式为![]() ,
,
由OP∥BD得直线BD的斜率为![]() ,
,
结合点B的坐标(6,0),得直线BD的表达式为![]() .
.
由 得,
得,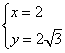 ,
,
∴点D的坐标为![]() .
.
略








