如图1,在△ABC中,∠C=90°,BC=8,AC=6,直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在BC边上,腰DH落在AC边上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3.固定△ABC,将直角梯形DEFH以每秒1个单位长度的速度沿CB向右移动,当点D与点B重合时停止.设移动的时间为t秒,移动后的直角梯形为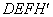 (如图2),△ABC与直角梯形
(如图2),△ABC与直角梯形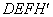 重叠部分的面积为S(这里规定点是面积为0的几何图形),则S与t之间的函数关系为( )
重叠部分的面积为S(这里规定点是面积为0的几何图形),则S与t之间的函数关系为( )
- A.
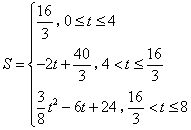
- B.
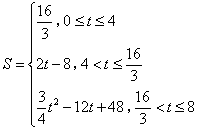
- C.
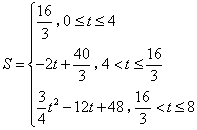
- D.
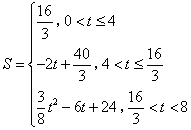
答案
正确答案:A
知识点:图形运动处理框架
1.解题要点
①研究基本图形,各线段长如图所示,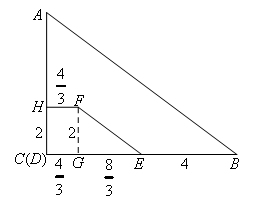
EF始终与AB平行.
②分析运动状态,如图所示,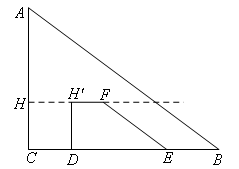
在找状态转折点时,找边与顶点碰撞的时刻,
∴![]() .
.
③分段画图,设计方案求解面积.
2.解题过程
由题意得,DH=2,DE=4,
过点F作FG⊥BC于点G,得到各线段长如下图所示,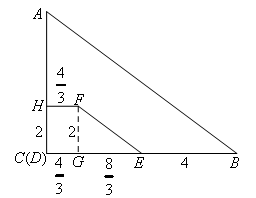
①当![]() 时,重叠部分即为直角梯形
时,重叠部分即为直角梯形![]() ,如图所示,
,如图所示,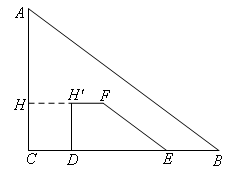
∵DE=4,![]() ,
,
∴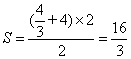 .
.
②当![]() 时,如图所示,
时,如图所示,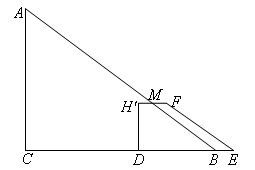
设![]() 与AB交于点M,则重叠部分为直角梯形
与AB交于点M,则重叠部分为直角梯形![]() ,
,
∵CE=t+4,BC=8,
∴BE=t-4.
∵重叠部分的面积S=梯形![]() 的面积-平行四边形MBEF的面积,
的面积-平行四边形MBEF的面积,
∴![]() .
.
③当![]() 时,如图所示,
时,如图所示,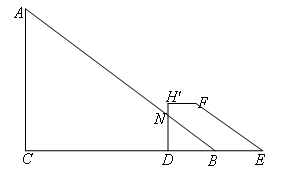
设![]() 与AB交于点N,则重叠部分为△BDN,
与AB交于点N,则重叠部分为△BDN,
∵CD=t,BC=8,
∴BD=8-t.
△BDN是三边之比为3:4:5的直角三角形,
∴![]() ,
,
∴![]() .
.
综上所述,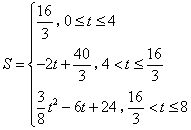 .
.
略








