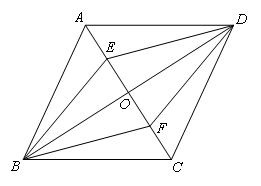
如图，在菱形ABCD中，对角线AC，BD相交于点O，E，F分别是OA，OC的中点．下列结论：①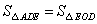；②四边形BFDE也是菱形；③△DEF是轴对称图形；④∠ADE=∠EDO；
⑤四边形ABCD面积为．其中正确的有(    )

结论①：
∵E是OA中点，由“背靠背结构”，可得，故①对．
结论②：
由菱形ABCD可得，OB=OD，OA=OC，BD⊥EF，
又E，F分别是OA，OC的中点，则OE=OF，
∴四边形BFDE也是菱形（对角线互相垂直的平行四边形是菱形），故②对．
结论③：
由②知，OE=OF，DO⊥EF，
则△DEF是等腰三角形，因此△DEF是轴对称图形，故③对．
结论④：
假设∠ADE=∠EDO，∵EA=EO，
∴AD=OD，
事实上，（直角三角形的斜边大于直角边），
矛盾，因此假设错误，故④错．
结论⑤：
，故⑤对．
综上，①、②、③、⑤对，故选B．

略