（上接第1题）（2）在四边形BMCA面积最大的条件下，过点M作y轴的平行线，若在这条平行线上存在点Q，使得以Q为圆心，OQ为半径的圆与直线AC相切，则点Q的坐标为(    )

由第1题的分析可知，当m=-2时，四边形BMCA的面积最大．
如图，设直线x=-2与x轴交于点G，与直线AC交于点H，
过点Q作QP⊥AC于点P．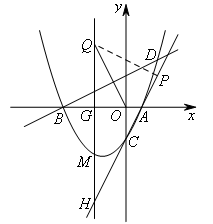

要使得题干要求成立，需QP=OQ．
由A（1，0），C（0，-2）得，直线AC的解析式为y=2x-2．
令x=-2，得y=-6，
∴H（-2，-6），GH=6．
在Rt△AGH中，由勾股定理得，．
设点Q的坐标为（-2，n），则，即．
当点Q在点H上方时，QH=n+6．
易证△AGH∽△QPH，
∴，即，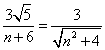
∴n=4或n=-1，
∴点Q的坐标为（-2，4）或（-2，-1）．
当点Q在点H下方时，易证．
综上得，点Q的坐标为（-2，4）或（-2，-1）．

略