如图,在平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A,O,B三点,M为线段OB下方的抛物线上一动点(不与点O,B重合).
(1)设△BOM的面积为S,则S的最大值为( )

- A.
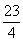
- B.
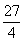
- C.
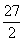
- D.
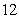
答案
正确答案:B
知识点:二次函数背景下的面积问题 面积处理思路 函数处理框架
1.解题要点
①由A,B,O三点坐标,可得抛物线解析式.
②研究基本图形,可以得到OA⊥OB,
点A和点B分别在第一、三,二、四象限的角平分线上.
③研究目标△BOM,是斜放置的三角形,且是两定点一动点,
所以采用铅垂法表达面积,过动点M作平行于y轴的直线.
④注意点M的横坐标的取值范围.
2.解题过程
设抛物线的解析式为![]() ,
,
∵点A(-2,2),B(6,6)在抛物线上,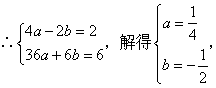
∴![]() ,
,![]() .
.
如图,过点M作MN∥y轴,交线段OB于点N.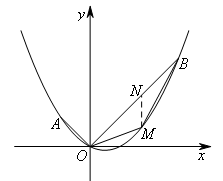
设点M的横坐标为![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴当![]() 时,
时,![]() .
.
此时![]() .
.
略








