在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且CE=DE．为判断AE和BD之间的关系，小明准备分情况进行讨论．
当E是AB中点时，如图1，

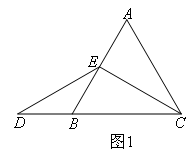
小明发现，由于E是AB边的中点，利用三线合一可以得到AE=BE，∠ECB=30°，
再由CE=DE可以得到∠D=30°，进而得到∠BED=30°，就可以得到BD=BE=AE．
但是当E不是AB中点时，就不能照搬上述方式进行证明，此时小明想到了另外一种方式：
过点E作EF∥BC，交AC于点F，也能证明AE=BD．
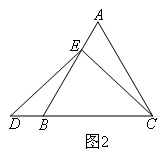
（1）当E是线段AB上除端点和中点外的任一点时，如图2，按照上述辅助线证明AE=BD，证明过程中需要使用一对三角形全等，则证明此对三角形全等不能使用的条件是(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=13004
1．解题要点
①要在图2中照搬小明的思路，需要明白小明的思路在图1中是怎么证明的．
考虑不能利用E是中点带来的结论，
所以证明时，要避开中点带来的结论（AE=BE，∠ECB=30°），用其他条件来讨论．

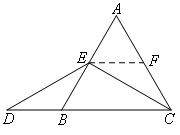
过点E作EF∥BC，交AC于点F，则△AEF是等边三角形，AE=EF=AF，
能够证明△EFC≌△DBE，EF=BD，进而得到AE=BD．
②在图2中，同样作出辅助线，如图所示，

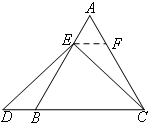
照搬①中的证明思路，先得到△AEF是等边三角形，AE=EF，再证明△EFC≌△DBE．关键在于判断三角形全等能够使用的条件有哪些．
由题意得，BE=FC．
∵∠ABC=∠AFE=60°，
∴∠DBE=∠EFC=120°．
∵∠D+∠DEB=60°，∠ECD+∠ECF=60°，∠D=∠ECD，
∴∠DEB=∠ECF．
同时∠D=∠ECD=∠CEF，
即两个三角形中，三组内角分别对应相等，同时BE=CF，CE=DE，
则证明△EFC≌△DBE可以使用AAS，ASA，SAS，不能使用的是SSS．
③思考前面的证明过程，不变的特征是：△ABC是等边三角形，CE=DE．
作平行线是为了得到等边三角形，进而得到全等三角形．
④整个证明的路线图是：作辅助线；判断等边三角形（△AEF）；证明△EFC≌△DBE．
2．解题过程
我们利用SAS来证明AE=BD，具体过程如下：
如图，过点E作EF∥BC，交AC于点F．

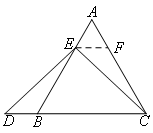
则∠AEF=∠ABC=∠A=60°，
∴△AEF是等边三角形，
∴AE=EF=AF，
∴BE=FC．
∵CE=DE，
∴∠D=∠ECD．
∵∠ABC=∠ACB，
∴∠D+∠DEB=∠ECD+∠ECF，
∴∠DEB=∠ECF，
∴△EFC≌△DBE（SAS），
∴EF=BD，
∴AE=BD．

略