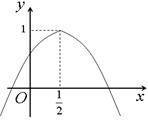
如图，二次函数y=ax²+bx+c的图象与y轴正半轴相交，其顶点坐标为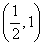，下列结论：
①ac＜0；②a+b=0；③4ac－b²=4a；④a+b+c＜0.其中正确的个数是（）

①设y=ax2+bx+c=0时两根为、，在的左边，则<0,>0，故=c/a<0,即得ac<0；
②对称轴为-b/2a=1/2,即得a+b=0；
③顶点坐标（-b/2a，(4ac－b²)/4a）即(4ac－b²)/4a=1，得4ac－b²=4a；
④由对称轴为x=1/2，<0,>0知>1,故当x=1时y=a+b+c>0。
则①②③正确，④错误；

略