如图1，在等腰直角三角形ABC和等腰直角三角形CDE中，CD>BC，点C，B，D在同一直线上，M是AE的中点，易证MD⊥MB，MD=MB．

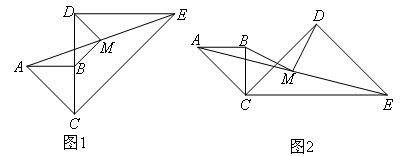
（1）如图2，将图1中的△CDE绕点C顺时针旋转45°，使△CDE的斜边CE恰好与△ABC的边BC垂直．题干中的其他条件不变，若要证明MD⊥MB，MD=MB，需要证明两次三角形全等．则判定第二次三角形全等使用的条件是(    )

1．解题要点
①首先需要弄明白图1中的结论是如何证明的．
M是AE的中点，AB∥DE，有“平行+中点”的结构，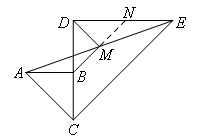

所以延长BM，交DE于点N，可以得到△ABM≌△ENM．
进而得到BM=MN，AB=BC=EN，
∴DN=DB，
∴△DBN是等腰直角三角形，
∴MD⊥MB，MD=MB．
②图2中，M是AE的中点，AB∥CE，补全“平行+中点”的结构，照搬图1中的证明思路．
延长BM，交CE于点N，连接BD，DN，能够得到△ABM≌△ENM，BM=MN，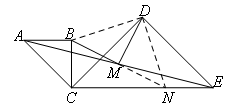

要证明△DBN是等腰直角三角形，需要证明△BCD≌△NED，利用SAS可以证明．
③图1和图2中没有发生变化的是“两个三角形是等腰直角三角形，M是AE的中点”．
④整个证明的路线图是：
构造“平行+中点”的辅助线；
△ABM≌△ENM；
△BCD≌△NED；
△DBN是等腰直角三角形，证明结论成立．
2．解题过程
如图，延长BM，交CE于点N，连接BD，DN．

∵BC⊥CE，AB⊥BC，
∴AB∥CE．
∵AM=EM，∠AMB=∠EMN，
∴△ABM≌△ENM，
∴BM=MN，BC=AB=EN．
∵∠BCD=∠NED=45°，CD=ED，
∴△BCD≌△NED（SAS），
∴∠BDC=∠NDE，BD=ND．
∵∠NDE +∠CDN=90°，
∴∠BDC+∠CDN=90°，即∠BDN=90°．
∴△DBN是等腰直角三角形．
∵BM=MN，
∴MD⊥MB，MD=MB．

略